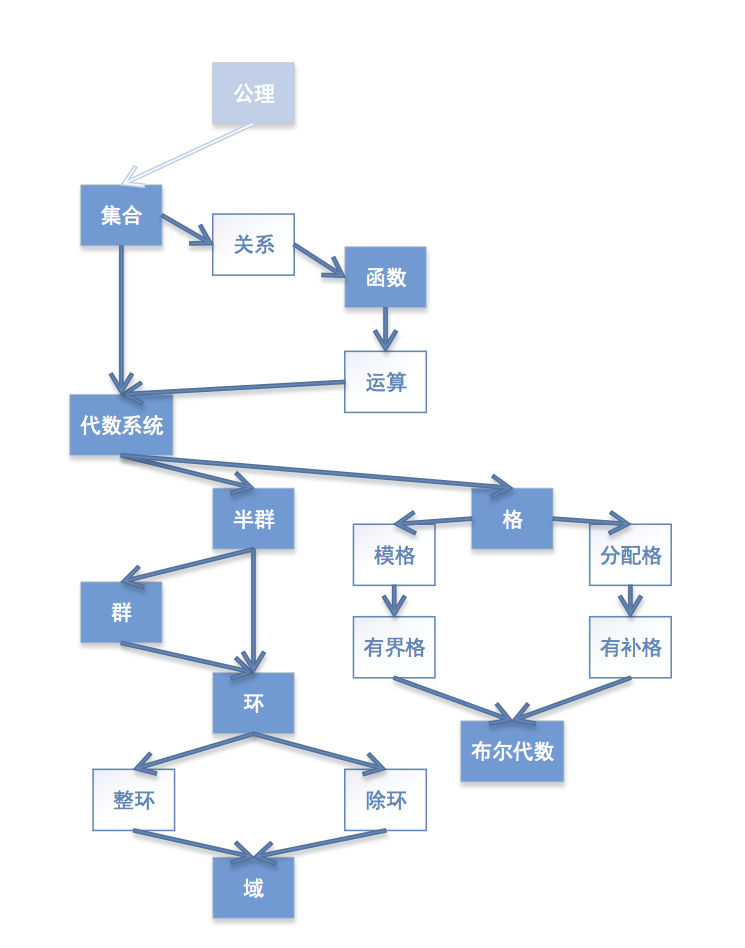
每一次画示意图，我都发誓这是我最后一次画示意图。神呐救救我的布局吧。

1. 集合的性质是由公理得出的。
2. 两个集合的叉积（笛卡尔积）的一个子集称为这两个集合上的关系。
   • 等价关系的证明：自反、对称、传递。
   • 半序关系的证明：自反、反对称、传递。
3. 函数的证明：左满右唯一。
4. 运算的证明：封闭性。
   1. 通常出现在群上运算的规律：结合律，交换律，分配率。
      • 对于某两个运算$\otimes$和$\oplus$，则$\otimes$对$\oplus$的分配率：$a \otimes (b \oplus c) = (a \otimes c) \oplus (b \otimes c)$。注意哪一个在里面。
   2. 通常出现在格上运算的规律：吸收率，幂等律，交换律，结合律，模律。模律是对称的。
   3. 通常出现在群上运算的特殊元素：零元、幺元、零因子、逆元、生成元。
   4. 通常出现在格上运算的特殊元素：补元。
   5. 通常用来组成群上运算的基本运算：加、乘、模加、模乘。
   6. 通常用来组成格上运算的基本运算：最大公约数、最小公倍数、交（与）、并（或）、补（非）。
5. 代数系统的证明：运算封闭。
   • 子代数系统证明：非空、包含、运算封闭。
6. 半群的证明：运算封闭、结合律。
   • 子半群的证明：非空、包含、运算封闭。（结合律继承）
7. 群的证明：运算封闭、结合律、有幺元、每个元素都有逆元。
   • 子群的证明：非空、包含、幺元属于子集、运算的混合封闭性：$\forall x,y \in S,\, x \oplus y^{-1} \in S$。（结合律继承）

剩下的还没复习完，未完待续。